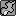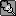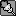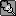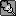As you might know, I was researching into a method of finding the centralisation of a metagame as a number. Refer to these two threads.
At the conclusion of the former thread, I finally found a good measurement, though not for centralisation, but for diversity, which can be understood as being inversely proportional to centralisation. The method of measurement is repeated here.
First, we convert each Pokemon usage U_i in descending order to the probability of it being in a team. This is done by multiplying it by 6 and dividing it by the sum of all usages U. This number, incidentally, is related to how much that Pokemon is centralising in that metagame; the higher it is, the more centralising is that Pokemon. In fact, we can define it as being the centralisation of that particular Pokemon in that metagame.
Then start summing up all these numbers until the answer first exceeds 5, and count all the numbers summed up. This would be the diversity D of the metagame.
From the definition above, it is clear that the lowest value D can have is 6 (if all teams are the same), and the highest value it can be is one more than 5/6 of the number of Pokemon in that metagame (if all usages are the same). Thus, we can find the percentage diversity which gives us the level of diversity of that metagame compared to the number of Pokemon it contains. We basically would like this percentage to be 0% if D=6 and to be 100% if D = 1 + 5P/6, where P is the number of Pokemon in that metagame. This is achieved by:
This assumes that a metagame has more than 6 possible Pokemon to choose from. In a metagame having 6 Pokemon, the measure of diversity would be meaningless, as every team will be forced to contain exactly those 6 Pokemon. Hence the (P-6) in the denominator poses no trouble whatsoever.
The above measurement isn't very important from the actual diversity's point of view; it is only interesting as a way to compare different metagames.
So, to summarise:
So we don't have a formula for centralisation, but we have one for diversity. :)
Here is a table containing the diversity of each metagame from July to November:
And this is a table containing the percentage diversities, which is less important than the above, but is interesting to find the percentage of diversity with respect to the number of Pokemon in that metagame:
At the conclusion of the former thread, I finally found a good measurement, though not for centralisation, but for diversity, which can be understood as being inversely proportional to centralisation. The method of measurement is repeated here.
First, we convert each Pokemon usage U_i in descending order to the probability of it being in a team. This is done by multiplying it by 6 and dividing it by the sum of all usages U. This number, incidentally, is related to how much that Pokemon is centralising in that metagame; the higher it is, the more centralising is that Pokemon. In fact, we can define it as being the centralisation of that particular Pokemon in that metagame.
Then start summing up all these numbers until the answer first exceeds 5, and count all the numbers summed up. This would be the diversity D of the metagame.
From the definition above, it is clear that the lowest value D can have is 6 (if all teams are the same), and the highest value it can be is one more than 5/6 of the number of Pokemon in that metagame (if all usages are the same). Thus, we can find the percentage diversity which gives us the level of diversity of that metagame compared to the number of Pokemon it contains. We basically would like this percentage to be 0% if D=6 and to be 100% if D = 1 + 5P/6, where P is the number of Pokemon in that metagame. This is achieved by:
Code:
Percentage Diversity PD = 120 x (D-6) / (P-6)The above measurement isn't very important from the actual diversity's point of view; it is only interesting as a way to compare different metagames.
So, to summarise:
Code:
C_i = 6 x U_i / U
D is the smallest number of C_i's that, when summed up together, the answer is greater than 5.
PD = 120 x (D-6) / (P-6)
where C_i is the centralisation of Pokemon i
U_i is the usage of Pokemon i
U is the sum of all Pokemon usages
D is the diversity of a metagame
PD is the percentage diversity of a metagame
P is the number of Pokemon in the metagameHere is a table containing the diversity of each metagame from July to November:
Code:
Ladder Diversity
Jul Aug Sep Oct Nov
------------------------------------
Standard 60 63 67 62 66
UU 52 61 65 58 55
Uber 22 25 27 23 24
Suspect -- 54 52 41 --
CAP -- -- 59 -- 51
Little Cup -- -- 27 -- 30
Code:
Ladder Percentage Diversity
Jul Aug Sep Oct Nov
---------------------------------------------------------
Standard 13.76% 14.52% 15.38% 14.12% 15.16%
UU 20.60% 24.63% 26.42% 23.28% 21.94%
Uber 3.91% 4.64% 5.06% 4.10% 4.34%
Suspect --- 12.28% 11.62% 8.82% ---
CAP --- --- 13.25% --- 11.25%
Little Cup --- --- 15.85% --- 18.11%