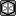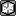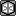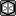This is a continuation of this thread. There, I tried to measure the centralisation of a metagame using just two numbers. This was overly simplistic, unfortunately, and, while that formula produced pretty adequate numbers, it wasn't good enough (see my penultimate post in that thread and the post before it to see why).
One of the problems was that I didn't take the number of legal Pokemon in a particular metagame into account. This is actually very important. If a metagame has 100 Pokemon and each were used, say, 1000 times, that metagame has zero centralisation. However, if another metagame has 100 Pokemon where 10 of them were used 10000 times and the other 90 weren't used at all, that metagame is much more centralised. This very simple thing is something that the previous formula didn't address at all, which is something that kind of makes me ashamed when I think about it... :|
Anyway, back to the new formula. As I said before, if all Pokemon were used equally, then the centralisation would be zero. Thus, suppose the total number of usages is U and the number of Pokemon in a metagame is P. For a completely uncentralised metagame, each of the P Pokemon would be expected to be used U/P times.
Of course, in reality, there would be Pokemon that would be used more than U/P times and others that would be used less than U/P times, and this would give us an element of centralisation depending on how far the deviation from the U/P is for each Pokemon. So I defined the centralisation of a metagame to be this deviation.
So basically, the centralisation of a metagame is almost the same as the standard deviation of all usages, except that, instead of finding the deviation from the mean of the usages, we find the deviation from the number U/P. Rearranging this equation to simplify it and multiplying it by 100 to get a more manageable number, we get:
Using this formula, here are the centralisation numbers for all metagames from July to November:
One of the problems was that I didn't take the number of legal Pokemon in a particular metagame into account. This is actually very important. If a metagame has 100 Pokemon and each were used, say, 1000 times, that metagame has zero centralisation. However, if another metagame has 100 Pokemon where 10 of them were used 10000 times and the other 90 weren't used at all, that metagame is much more centralised. This very simple thing is something that the previous formula didn't address at all, which is something that kind of makes me ashamed when I think about it... :|
Anyway, back to the new formula. As I said before, if all Pokemon were used equally, then the centralisation would be zero. Thus, suppose the total number of usages is U and the number of Pokemon in a metagame is P. For a completely uncentralised metagame, each of the P Pokemon would be expected to be used U/P times.
Of course, in reality, there would be Pokemon that would be used more than U/P times and others that would be used less than U/P times, and this would give us an element of centralisation depending on how far the deviation from the U/P is for each Pokemon. So I defined the centralisation of a metagame to be this deviation.
So basically, the centralisation of a metagame is almost the same as the standard deviation of all usages, except that, instead of finding the deviation from the mean of the usages, we find the deviation from the number U/P. Rearranging this equation to simplify it and multiplying it by 100 to get a more manageable number, we get:
Code:
Central = 100 x sqrt(Sum_i(((U_i/U) - (1/P))^2))
where U_i is the usage of Pokemon i
U is the sum of all usages
P is the number of Pokemon in the metagame
Code:
Ladder Months
Jul Aug Sep Oct Nov
------------------------------------------
Standard 13.0 12.6 11.7 12.4 11.9
UU 12.2 11.2 10.7 11.4 12.4
Uber 21.3 19.9 19.7 20.3 20.2
Suspect -- 13.2 13.4 15.5 --
CAP -- -- 12.3 -- 15.4
Little Cup -- -- 17.9 -- 16.4