This post has been revised to reflect the current state of Pokemon Showdown rating systems
Many users have no understanding of how a rating system works or its fundamental limitations. This article, which could either go in the forums alongside the Weighted Stats FAQ or on-site somewhere, was written to educate members of the community about our rating system, to answer fundamental questions about how it works and, ideally, to lead to a more informed discussion of our ladder practices. I welcome any and all constructive feedback, especially questions that will help populate the FAQ section.
-------------------------
Introduction
Rating systems and ladders are a fundamental component of many competitive games, from college football to tennis to chess to competitive Pokemon. Pokemon Showdown, like other online games like League of Legends or Overwatch, implements a rating system to attempt to rank players based on skill and to pair players with similar skill levels for battles. This is not an easy job, and there is not a system on the planet that can do it perfectly. In what follows, I will be attempting to explain the concepts, theory and execution behind Showdown's rating system (and will in the process explain Pokemon Online's as well). For those who are mathematically inclined, I will include technical details. For those of you who aren't, this article was written so as to allow you to skip those sections without negatively impacting your ability to understand the rest of the article.
Background and History
The goal of most rating system is, most fundamentally, to determine a player's skill level. This can be useful for ranking players, for tournament seeding, or for pairing players of similar skill levels for optimally "interesting" battles, but at the end of the day, the goal is simply to try to determine how good a given player is, to the greatest degree of accuracy.
This is not a new problem, and competitive leagues have been at this for hundreds of years. Easily the simplest rating system is the win-loss record, but that has the problem of rewarding players who only play poor players and punishing those who seek out challenging opponents. Throughout the centuries, more complex points-based systems have been developed to try to correct for this issue but were often criticized as being arbitrary and unfair. Then in 1960, the United States Chess Federation adopted a new rating system designed by chess master and physicist Arpad Elo. His statistics-based rating system became widely popular due to its simplicity and fairness, and half a century later, almost all modern rating systems are built upon his concepts. Pokemon Online and Pokemon Showdown both use variants on Elo as their primary rating systems, although Showdown also implements an extension of Elo called Glicko (more on that in a bit). Older versions of Pokemon Showdown and the old Shoddy Battle used the Glicko-2 rating system, which is an extension of Glicko.
Ratings, Parameters and Estimates
I would say that 90% of people's confusion regarding the various ladders comes down to a lack of conceptual understanding concerning the difference between parameters and estimates. The issue is that a player's true skill level, the piece of information that all rating systems are fundamentally trying to determine, is fundamentally unknowable--there is no realistic way to have every player battle every other player on the ladder, and if there were, there would be no way to guarantee that the same matchup, if repeated, would have the same results. Instead, we have to approximate a player's skill level based on observation of the battles that actually took place.
In the language of statistics, a player's skill level is a "parameter"--if you know that, you know everything about how the player behaves. In contrast, the rating we generate based on the results of his or her battles is an "estimate" of this parameter. If you take nothing else away from this article, that is it, so I will repeat:
When most people think about climbing the ladder, they think of it in terms of earning "points" for wins and losing them for defeats. This leads to frustration when a highly ranked player sees his or her rating change not at all when they defeat a low-rated opponent (since they didn't gain any points by winning), but this is a mistake in thinking--the "reward" for the highly-rated player is that he or she has had his or her skill estimate "validated"--he or she has successfully shown that the ladder was justified in rating him or her so highly. This is something that bears emphasizing:
I realize that the above statement may be shocking--the idea that a player should be "rewarded" for battling more is ingrained into most players' psyches. And certainly, we want to encourage players to battle more frequently. What we don't want is players who reach the top of the ladder and "park" there, refusing to battle anyone further, for fear of losing his or her #1 spot when he or she suffer an unlucky defeat, and this is something I will discuss further in a later section. In the meantime, remember that the fundamental purpose of a ladder is not to reward or to punish, but to determine the skill levels of the players on it.
Both Glicko and Elo ratings are estimates of a player's skill, and in the sections that follow, I will explain some of the mechanics underlying these systems and explain how you should interpret your ratings.
Pokemon as a Different Sort of Card Game
Before I get into describing the rating systems themselves, I'm going to describe the mathematical theory at the heart of both systems. If you're not interested in the technical details, feel free to simply skip this section.
An important feature of most rating systems is that they do not require that a better player will always defeat an inferior one. Whether due to chance ("hax") or one player being "in the zone" while another is having an off-day, there will always be some uncertainty regarding the outcome of a match between two players, even if their skill levels are well defined.
To account for this, the Elo and Glicko systems use at their heart a model of "pairwise comparison" called Bradley-Terry, which simplifies all Pokemon battles (or chess games or tennis matches) down to a simple game of chance:
Picture two players, sitting across from each other. Each has his or her own deck of cards, and each card is marked with a number. The players shuffle their decks, and on the count of three, each pulls a single card and places it on the table. The winner is the player whose card has the higher number. The key aspect of this model--and what makes it different from, say, a simple coin toss--is that the two players need not have identical decks, and if one player's deck is stacked with numbers that are generally higher, then that player will be more likely to win.
While this model obscures the thrill of a well-made prediction and the frustration of an unfortunately-timed bit of hax, the point is that it's built into the model that a player will not always have the same "performance" every time he or she plays the game, even if his or her skill level hasn't changed, and the up-shot is that there's always a chance that an inferior player will defeat a superior one.
The Unknowable "True Rating"
The underlying principle behind both Elo and Glicko is that a player has a single "parameter" representing his or her skill level, and that parameter governs how the player will perform: as per the previous section, a player at a given skill level will sometimes end up performing under his or her skill level and sometimes over (due to luck, "hax" or simply being "in the zone"), but given enough battles, his or her "average" performance should converge to a well defined value. This average, or expected, performance I will refer to as the player's "true rating." This "true rating" is the end-all, be-all, the holy grail of ratings. Given two player's rating, it is, in principle, trivial to calculate the odds that one will defeat the other, and it is the goal of both the Elo and Glicko rating systems to estimate a player's "true rating" as closely and as accurately as possible. An important point here is that ratings are absolute--there's no "rock-paper-scissors" element here where Player A usually defeats Player B, Player B usually defeats Player C, but Player C usually defeats Player A--if Player A usually defeats Player B, and Player B usually defeats Player C, then it's assumed that Player A will usually defeat Player C as well.
The Elo Rating System
I'll start with Elo, which is the system behind the Pokemon Online and Pokemon Showdown ladders. Given a series of wins and losses against a collection of opponents, a player's Elo rating is calculated so as to be the "true rating" that has the greatest likelihood of producing those results. Keep in mind, once again, that sometimes a less skilled player will defeat a more-skilled one, so if you defeat three players with 1200 ratings and then proceed to lose to a player with an 800 rating, that's fine, Elo can account for that (what exactly your rating would be in that case depends on a choice of parameter).
Without going to go into details about how Elo ratings are actually calculated or updated, one of its main advantages is its simplicity (you can readily calculate how two players' ratings will change as a result of a single match) and transparency. For those used to points-based rating systems where ones rating goes up or down as a direct consequence of winning or losing, Elo feels comforting, aside from the extremes where a player with a much higher rating than his or her opponent will not gain any points from a victory. It was this simplicity and it's "fairness" and accuracy when compared to previously-used points-based rating systems that led to its wide-scale adoption, and after more than fifty years, its ubiquity is one of its big selling points.
Elo does have a number of downsides, though, the most prominent being that players with high ratings often have little incentive to continue playing and GREAT incentive NOT to play: if you have an rating of 1800 on PO and you end up facing a player with a rating of 1000, a loss will knock 50 points off your rating, whereas a win will net you zero. Consequently, it is not uncommon for top players on Elo-based ladders to "park" themselves at the top and refuse to continue battling altogether. To combat this, Pokemon Online introduced rating decay, which automatically lowers a player's displayed rating for every so-many hours the player stays inactive. Note that this doesn't actually change the player's rating, only what is displayed, and after a few battles, this decay is erased. This system effectively forces players to keep battling to retain their ranking, but there are other related issues that must be guarded against.
Pokemon Showdown's Elo implementation also includes a few tweaks, such as its own decay and a sliding "K-factor" which makes a player gain or lose fewer points the higher his or her Elo score.
The Glicko Rating System
In 1995, Mark Glickman, a statistician who is currently the chair of the United States Chess Federation's Ratings Committee, introduced an extension of the Elo rating system which he called Glicko (which was later extended to Glicko-2). Whereas Elo estimates a player's "true rating" by using only a single value, the player's rating, Glicko adds a second value, called RD (short for "rating deviation"), which quantifies the level of uncertainty in the estimate of a player's "true rating" (Glicko-2 adds on one more variable, called volatility, which measures the erraticness of a player's performance).
Thus, where Elo attempts to directly estimate a player's "true rating," Glicko instead estimates that a player's "true rating" falls within a probability distribution, in this case, a normal distribution of width RD and center R.
Below are two sample distributions: one for a player of rating 1600±100 and one whose rating is 1575±50.
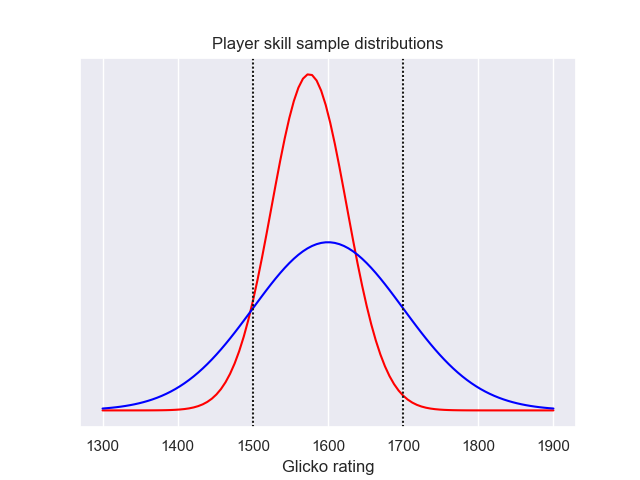 For those unfamiliar with probability distributions, the idea is that the probability of a player's "true rating" being in the infinitesimal interval r<rating<r+dr is f(r)dr.
For those unfamiliar with probability distributions, the idea is that the probability of a player's "true rating" being in the infinitesimal interval r<rating<r+dr is f(r)dr.
So looking at these two graphs the question is, who's the better player? Using the Glicko system, it's impossible to know for certain, but what we can determine is the likelihood that each player's "true rating" is above some specific value. For instance, in the case pictured above, there's an 84% chance that the blue player's "true rating" is above 1500 and a 93% chance that the same is true for the red player. On the other hand, there's less than a 1% chance that the red player's true rating is at least 1700, whereas the odds that the blue player is at least at that skill level is nearly 16%.
This showcases the primary problem with Glicko rating systems--whereas under Elo, comparing players was a simple matter of comparing their ratings, under Glicko it's much harder. In addition, Glicko ratings are updated only once per "rating period" (Showdown uses two days or 15 battles). Since players for the most part wouldn't stand for only seeing their ratings change every fifteen battles, players are assigned "provisional" ratings at the end of each battle which are designed to estimate how the new ratings will change. This can lead to confusion when a rating period ends, and the player's rating actually updates.
As with Elo, I won't be going into the technical details concerning implementation, although I will point out a key feature of Glicko: where Elo ladders have to manually implement rating decay to discourage periods of inactivity, Glicko builds inactivity into the rating system, with RD increasing the longer a player remains inactive.
Rating Estimates
So I said that since a player's Glicko rating is not one number but two, it's not nearly as straightforward to directly compare two players' skill levels. Ideally, a player's skill level would always be represented by his or her R and RD, and applications requiring an assessment of a player's skill level would be implemented probabilistically (see: Weighted Stats). Back in the real world, however, things like ladder rankings require us to have a set method of comparing two players and determining which one is "better." The way we do this is through "Conservative Rating Estimates" or CREs. CREs basically say, "I don't know for certain how good a player is, but I'm pretty sure he or she is better than this.
The most famous of these around here is ACRE, which was what Showdown's ladder used to use to rank players. ACRE (the "A" stands for "advanced") corresponds to about the 8th percentile of a player's rating distribution, meaning there's about a 92% chance that a player's "true rating" is at least as high as his or her ACRE. ACRE (and other CREs) is designed to be close to a player's real rating when they've played a lot of games (and Glicko is confident about their rating), and much lower if they haven't (and Glicko isn't confident). Other than that, it has the same problems Elo and Glicko has, with ratings not changing much on wins when you're at the top of the ladder.
One proposed alternative was designed for Smogon's Shoddy ladder by X-Act, a mathematician who was very active in the community in those days. His Glicko-X-Act Estimate (or GXE) measures the odds that a player would win a battle against a randomly selected opponent from the ladder. Players' GXEs are displayed along with their Elo and Glicko ratings on the Showdown ladder. While GXE is designed to have concrete meaning, it also does not fix the problem with wins not changing rating much. That being said, GXE is the primary component of COIL, an achievement-centric ladder score we previously used to determine suspect voting requirements.
There's an important point that bears emphasis about GXE and ACRE: people often erroneously refer to these rating estimates as if they were alternatives to Glicko, the same way Elo and Glicko are different rating systems, but in truth:
Quick note: Trueskill
Microsoft's Trueskill is another rating system that's been gaining traction lately, and it is occasionally suggested that PS implement Trueskill for its ladder. The problem is that Trueskill is proprietary (read: might require a license) and the differences between Trueskill and Glicko are mostly trivial.
Summary
At the end of the day, if you come away with nothing else after reading this article, I hope it's the following:
Further Reading
Ask away!
Many users have no understanding of how a rating system works or its fundamental limitations. This article, which could either go in the forums alongside the Weighted Stats FAQ or on-site somewhere, was written to educate members of the community about our rating system, to answer fundamental questions about how it works and, ideally, to lead to a more informed discussion of our ladder practices. I welcome any and all constructive feedback, especially questions that will help populate the FAQ section.
-------------------------
Introduction
Rating systems and ladders are a fundamental component of many competitive games, from college football to tennis to chess to competitive Pokemon. Pokemon Showdown, like other online games like League of Legends or Overwatch, implements a rating system to attempt to rank players based on skill and to pair players with similar skill levels for battles. This is not an easy job, and there is not a system on the planet that can do it perfectly. In what follows, I will be attempting to explain the concepts, theory and execution behind Showdown's rating system (and will in the process explain Pokemon Online's as well). For those who are mathematically inclined, I will include technical details. For those of you who aren't, this article was written so as to allow you to skip those sections without negatively impacting your ability to understand the rest of the article.
Background and History
The goal of most rating system is, most fundamentally, to determine a player's skill level. This can be useful for ranking players, for tournament seeding, or for pairing players of similar skill levels for optimally "interesting" battles, but at the end of the day, the goal is simply to try to determine how good a given player is, to the greatest degree of accuracy.
This is not a new problem, and competitive leagues have been at this for hundreds of years. Easily the simplest rating system is the win-loss record, but that has the problem of rewarding players who only play poor players and punishing those who seek out challenging opponents. Throughout the centuries, more complex points-based systems have been developed to try to correct for this issue but were often criticized as being arbitrary and unfair. Then in 1960, the United States Chess Federation adopted a new rating system designed by chess master and physicist Arpad Elo. His statistics-based rating system became widely popular due to its simplicity and fairness, and half a century later, almost all modern rating systems are built upon his concepts. Pokemon Online and Pokemon Showdown both use variants on Elo as their primary rating systems, although Showdown also implements an extension of Elo called Glicko (more on that in a bit). Older versions of Pokemon Showdown and the old Shoddy Battle used the Glicko-2 rating system, which is an extension of Glicko.
Ratings, Parameters and Estimates
I would say that 90% of people's confusion regarding the various ladders comes down to a lack of conceptual understanding concerning the difference between parameters and estimates. The issue is that a player's true skill level, the piece of information that all rating systems are fundamentally trying to determine, is fundamentally unknowable--there is no realistic way to have every player battle every other player on the ladder, and if there were, there would be no way to guarantee that the same matchup, if repeated, would have the same results. Instead, we have to approximate a player's skill level based on observation of the battles that actually took place.
In the language of statistics, a player's skill level is a "parameter"--if you know that, you know everything about how the player behaves. In contrast, the rating we generate based on the results of his or her battles is an "estimate" of this parameter. If you take nothing else away from this article, that is it, so I will repeat:
The rating shown on a ladder is simply an estimate of a player's skill level, nothing more.
When most people think about climbing the ladder, they think of it in terms of earning "points" for wins and losing them for defeats. This leads to frustration when a highly ranked player sees his or her rating change not at all when they defeat a low-rated opponent (since they didn't gain any points by winning), but this is a mistake in thinking--the "reward" for the highly-rated player is that he or she has had his or her skill estimate "validated"--he or she has successfully shown that the ladder was justified in rating him or her so highly. This is something that bears emphasizing:
Your rating is not something that you "earn." It is something you discover about yourself.
I realize that the above statement may be shocking--the idea that a player should be "rewarded" for battling more is ingrained into most players' psyches. And certainly, we want to encourage players to battle more frequently. What we don't want is players who reach the top of the ladder and "park" there, refusing to battle anyone further, for fear of losing his or her #1 spot when he or she suffer an unlucky defeat, and this is something I will discuss further in a later section. In the meantime, remember that the fundamental purpose of a ladder is not to reward or to punish, but to determine the skill levels of the players on it.
Both Glicko and Elo ratings are estimates of a player's skill, and in the sections that follow, I will explain some of the mechanics underlying these systems and explain how you should interpret your ratings.
Pokemon as a Different Sort of Card Game
Before I get into describing the rating systems themselves, I'm going to describe the mathematical theory at the heart of both systems. If you're not interested in the technical details, feel free to simply skip this section.
An important feature of most rating systems is that they do not require that a better player will always defeat an inferior one. Whether due to chance ("hax") or one player being "in the zone" while another is having an off-day, there will always be some uncertainty regarding the outcome of a match between two players, even if their skill levels are well defined.
To account for this, the Elo and Glicko systems use at their heart a model of "pairwise comparison" called Bradley-Terry, which simplifies all Pokemon battles (or chess games or tennis matches) down to a simple game of chance:
Picture two players, sitting across from each other. Each has his or her own deck of cards, and each card is marked with a number. The players shuffle their decks, and on the count of three, each pulls a single card and places it on the table. The winner is the player whose card has the higher number. The key aspect of this model--and what makes it different from, say, a simple coin toss--is that the two players need not have identical decks, and if one player's deck is stacked with numbers that are generally higher, then that player will be more likely to win.
While in principle, the distributions of cards in the deck could follow any form, in the Bradley-Terry model, the distribution of cards follows the Extreme Value (or Fisher-Tippett) distribution, which is asymmetric about its mean, having a longer positive "tail." This says that it is more likely that a player will occasionally play far above their typical skill level than it will be for them to play far below it. Furthermore, Elo (and consequently Glicko) assumes that these Extreme Value distributions have the same width and vary only by their center.
While this model obscures the thrill of a well-made prediction and the frustration of an unfortunately-timed bit of hax, the point is that it's built into the model that a player will not always have the same "performance" every time he or she plays the game, even if his or her skill level hasn't changed, and the up-shot is that there's always a chance that an inferior player will defeat a superior one.
The Unknowable "True Rating"
The underlying principle behind both Elo and Glicko is that a player has a single "parameter" representing his or her skill level, and that parameter governs how the player will perform: as per the previous section, a player at a given skill level will sometimes end up performing under his or her skill level and sometimes over (due to luck, "hax" or simply being "in the zone"), but given enough battles, his or her "average" performance should converge to a well defined value. This average, or expected, performance I will refer to as the player's "true rating." This "true rating" is the end-all, be-all, the holy grail of ratings. Given two player's rating, it is, in principle, trivial to calculate the odds that one will defeat the other, and it is the goal of both the Elo and Glicko rating systems to estimate a player's "true rating" as closely and as accurately as possible. An important point here is that ratings are absolute--there's no "rock-paper-scissors" element here where Player A usually defeats Player B, Player B usually defeats Player C, but Player C usually defeats Player A--if Player A usually defeats Player B, and Player B usually defeats Player C, then it's assumed that Player A will usually defeat Player C as well.
The Elo Rating System
I'll start with Elo, which is the system behind the Pokemon Online and Pokemon Showdown ladders. Given a series of wins and losses against a collection of opponents, a player's Elo rating is calculated so as to be the "true rating" that has the greatest likelihood of producing those results. Keep in mind, once again, that sometimes a less skilled player will defeat a more-skilled one, so if you defeat three players with 1200 ratings and then proceed to lose to a player with an 800 rating, that's fine, Elo can account for that (what exactly your rating would be in that case depends on a choice of parameter).
Without going to go into details about how Elo ratings are actually calculated or updated, one of its main advantages is its simplicity (you can readily calculate how two players' ratings will change as a result of a single match) and transparency. For those used to points-based rating systems where ones rating goes up or down as a direct consequence of winning or losing, Elo feels comforting, aside from the extremes where a player with a much higher rating than his or her opponent will not gain any points from a victory. It was this simplicity and it's "fairness" and accuracy when compared to previously-used points-based rating systems that led to its wide-scale adoption, and after more than fifty years, its ubiquity is one of its big selling points.
Elo does have a number of downsides, though, the most prominent being that players with high ratings often have little incentive to continue playing and GREAT incentive NOT to play: if you have an rating of 1800 on PO and you end up facing a player with a rating of 1000, a loss will knock 50 points off your rating, whereas a win will net you zero. Consequently, it is not uncommon for top players on Elo-based ladders to "park" themselves at the top and refuse to continue battling altogether. To combat this, Pokemon Online introduced rating decay, which automatically lowers a player's displayed rating for every so-many hours the player stays inactive. Note that this doesn't actually change the player's rating, only what is displayed, and after a few battles, this decay is erased. This system effectively forces players to keep battling to retain their ranking, but there are other related issues that must be guarded against.
Pokemon Showdown's Elo implementation also includes a few tweaks, such as its own decay and a sliding "K-factor" which makes a player gain or lose fewer points the higher his or her Elo score.
The Glicko Rating System
In 1995, Mark Glickman, a statistician who is currently the chair of the United States Chess Federation's Ratings Committee, introduced an extension of the Elo rating system which he called Glicko (which was later extended to Glicko-2). Whereas Elo estimates a player's "true rating" by using only a single value, the player's rating, Glicko adds a second value, called RD (short for "rating deviation"), which quantifies the level of uncertainty in the estimate of a player's "true rating" (Glicko-2 adds on one more variable, called volatility, which measures the erraticness of a player's performance).
Thus, where Elo attempts to directly estimate a player's "true rating," Glicko instead estimates that a player's "true rating" falls within a probability distribution, in this case, a normal distribution of width RD and center R.
Below are two sample distributions: one for a player of rating 1600±100 and one whose rating is 1575±50.
So looking at these two graphs the question is, who's the better player? Using the Glicko system, it's impossible to know for certain, but what we can determine is the likelihood that each player's "true rating" is above some specific value. For instance, in the case pictured above, there's an 84% chance that the blue player's "true rating" is above 1500 and a 93% chance that the same is true for the red player. On the other hand, there's less than a 1% chance that the red player's true rating is at least 1700, whereas the odds that the blue player is at least at that skill level is nearly 16%.
This showcases the primary problem with Glicko rating systems--whereas under Elo, comparing players was a simple matter of comparing their ratings, under Glicko it's much harder. In addition, Glicko ratings are updated only once per "rating period" (Showdown uses two days or 15 battles). Since players for the most part wouldn't stand for only seeing their ratings change every fifteen battles, players are assigned "provisional" ratings at the end of each battle which are designed to estimate how the new ratings will change. This can lead to confusion when a rating period ends, and the player's rating actually updates.
As with Elo, I won't be going into the technical details concerning implementation, although I will point out a key feature of Glicko: where Elo ladders have to manually implement rating decay to discourage periods of inactivity, Glicko builds inactivity into the rating system, with RD increasing the longer a player remains inactive.
Rating Estimates
So I said that since a player's Glicko rating is not one number but two, it's not nearly as straightforward to directly compare two players' skill levels. Ideally, a player's skill level would always be represented by his or her R and RD, and applications requiring an assessment of a player's skill level would be implemented probabilistically (see: Weighted Stats). Back in the real world, however, things like ladder rankings require us to have a set method of comparing two players and determining which one is "better." The way we do this is through "Conservative Rating Estimates" or CREs. CREs basically say, "I don't know for certain how good a player is, but I'm pretty sure he or she is better than this.
The most famous of these around here is ACRE, which was what Showdown's ladder used to use to rank players. ACRE (the "A" stands for "advanced") corresponds to about the 8th percentile of a player's rating distribution, meaning there's about a 92% chance that a player's "true rating" is at least as high as his or her ACRE. ACRE (and other CREs) is designed to be close to a player's real rating when they've played a lot of games (and Glicko is confident about their rating), and much lower if they haven't (and Glicko isn't confident). Other than that, it has the same problems Elo and Glicko has, with ratings not changing much on wins when you're at the top of the ladder.
One proposed alternative was designed for Smogon's Shoddy ladder by X-Act, a mathematician who was very active in the community in those days. His Glicko-X-Act Estimate (or GXE) measures the odds that a player would win a battle against a randomly selected opponent from the ladder. Players' GXEs are displayed along with their Elo and Glicko ratings on the Showdown ladder. While GXE is designed to have concrete meaning, it also does not fix the problem with wins not changing rating much. That being said, GXE is the primary component of COIL, an achievement-centric ladder score we previously used to determine suspect voting requirements.
There's an important point that bears emphasis about GXE and ACRE: people often erroneously refer to these rating estimates as if they were alternatives to Glicko, the same way Elo and Glicko are different rating systems, but in truth:
ACRE and GXE are measures for interpreting Glicko ratings and are not independent systems.
Quick note: Trueskill
Microsoft's Trueskill is another rating system that's been gaining traction lately, and it is occasionally suggested that PS implement Trueskill for its ladder. The problem is that Trueskill is proprietary (read: might require a license) and the differences between Trueskill and Glicko are mostly trivial.
Summary
At the end of the day, if you come away with nothing else after reading this article, I hope it's the following:
- Ratings are not rewards: while one's rating may go up after winning a battle and down after losing one, at the end of the day one's rating, as implemented on Pokemon Online and Pokemon Showdown is designed to be an accurate measure of one's skill level.
- It is important to differentiate between a player's "true rating," which is not knowable, his or her Glicko rating, which is not a single number but rather a rating an an uncertainty, RD, that together define the likelihood of his or her "true rating" falling within a given range, and a player's Rating Estimate, either expressed as ACRE or GXE, which whitewashes most of the nuances of your Glicko rating.
Further Reading
- For those interested in a more in-depth look at the theory behind statistical rating systems, and Elo in particular, I recommend this paper by Mark Glickman: http://www.glicko.net/research/acjpaper.pdf
- Here is a paper by Glickman's outlining his Glicko rating system: http://www.glicko.net/glicko/glicko.pdf
- And a paper describing Glicko-2: http://www.glicko.net/glicko/glicko2.pdf
Ask away!
Last edited by a moderator:





























