4. oregon wildfires
-
Check out the relaunch of our general collection, with classic designs and new ones by our very own Pissog!
-
Welcome to Smogon! Take a moment to read the Introduction to Smogon for a run-down on everything Smogon, and make sure you take some time to read the global rules.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Survivor Smogon Survivor: The Official (Started! Join server to spectate)
- Thread starter apricity
- Start date
not really, but i'll take it. the mountain is theri kaadu.task 4: Kudiraimozhi Mineral Deposits
2 engineering, 2 marketing, 1 finance. good night everyone!
Task 6:
What movie is the below image from?
Each tribe may guess once every 15 minutes.

Task 7:
366 people stand in an ordered line: none of whom were born on leap days, and all have randomly distributed birthdays. The host goes through the line in order and checks everyone’s birthday--when the host sees someone with a repeat birthday, he stops. With proof: at which position is he most likely to first stop?
Guess as many times as you'd like for this question, with one guess per post. Correct answers with incorrect proofs will be rejected, and I can be available to explain privately why the proof is wrong.
Task 8:
Within the next hour, submit one guess privately as a tribe as to how many mini m&ms are in this wine glass.
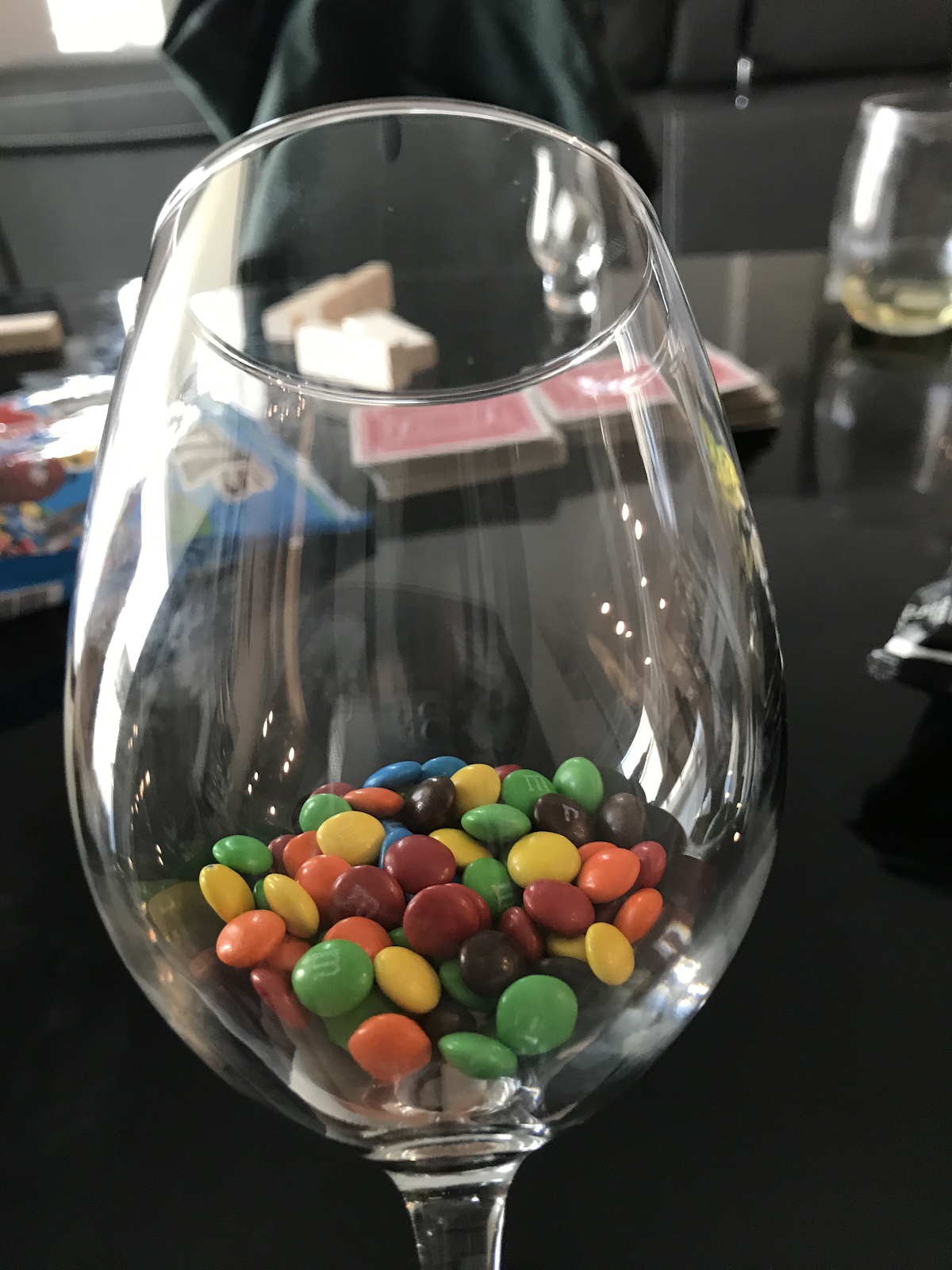

What movie is the below image from?
Each tribe may guess once every 15 minutes.
Task 7:
366 people stand in an ordered line: none of whom were born on leap days, and all have randomly distributed birthdays. The host goes through the line in order and checks everyone’s birthday--when the host sees someone with a repeat birthday, he stops. With proof: at which position is he most likely to first stop?
Guess as many times as you'd like for this question, with one guess per post. Correct answers with incorrect proofs will be rejected, and I can be available to explain privately why the proof is wrong.
Task 8:
Within the next hour, submit one guess privately as a tribe as to how many mini m&ms are in this wine glass.
the first person does not share a birthday with anyone
the second person has a 364/365 chance of not sharing a birthday with the first person
the third person has one less available day than the second person, and as such has a 363/365 chance of not sharing a birthday with either person in front of them, and so on.
Multiplying down the line, this calculates the probability of each person having a unique birthday relative to all people before them.
the host is will most likely stop when he has a greater than 50% chance of two people sharing a birthday
therefore the calculated probability must be lower than 0.5 when the host stops. this first occurs at 23 people when the probability is 0.4927 of all people having unique birthdays.
The probability formula is n!/n!(n-r!) where n is 365, the number of available days in the year to pick from and r is equal to the number of people being counted.
the second person has a 364/365 chance of not sharing a birthday with the first person
the third person has one less available day than the second person, and as such has a 363/365 chance of not sharing a birthday with either person in front of them, and so on.
Multiplying down the line, this calculates the probability of each person having a unique birthday relative to all people before them.
the host is will most likely stop when he has a greater than 50% chance of two people sharing a birthday
therefore the calculated probability must be lower than 0.5 when the host stops. this first occurs at 23 people when the probability is 0.4927 of all people having unique birthdays.
The probability formula is n!/n!(n-r!) where n is 365, the number of available days in the year to pick from and r is equal to the number of people being counted.
Task 7: 20. (A different example is used)
"
The probability, p(n)p(n), of getting a free ticket when you are the nthnth person is line is:
(probability that none of the first n−1n−1 people share birth dates) * (probability that you share birthday with one of the first n−1n−1 people)
So, p(n)=[1∗(364365)∗(363365)∗...∗((365−(n−2))365)]∗[(n−1)365]p(n)=[1∗(364365)∗(363365)∗...∗((365−(n−2))365)]∗[(n−1)365],
Here, 0<n≤3650<n≤365.
Now the least nn such that p(n)>p(n+1)p(n)>p(n+1), or p(n)p(n+1)>1p(n)p(n+1)>1.
Now, p(n)p(n+1)=365(366−n)∗(n−1)np(n)p(n+1)=365(366−n)∗(n−1)n
⟹365n−365>366n−n2⟹365n−365>366n−n2,
⟹n2−n−365>0⟹n2−n−365>0
⟹(n−(1+(√1461)2)∗(n−(1−(√1461)2)>0⟹(n−(1+(1461)2)∗(n−(1−(1461)2)>0
⟹n=(1+(√1461)2=19.6115148536⟹n=(1+(1461)2=19.6115148536 (∵n>0∵n>0)
⟹n=20⟹n=20 (ceiling of computed value)
Hence the 20th20th position maximizes the chances.
"
"
The probability, p(n)p(n), of getting a free ticket when you are the nthnth person is line is:
(probability that none of the first n−1n−1 people share birth dates) * (probability that you share birthday with one of the first n−1n−1 people)
So, p(n)=[1∗(364365)∗(363365)∗...∗((365−(n−2))365)]∗[(n−1)365]p(n)=[1∗(364365)∗(363365)∗...∗((365−(n−2))365)]∗[(n−1)365],
Here, 0<n≤3650<n≤365.
Now the least nn such that p(n)>p(n+1)p(n)>p(n+1), or p(n)p(n+1)>1p(n)p(n+1)>1.
Now, p(n)p(n+1)=365(366−n)∗(n−1)np(n)p(n+1)=365(366−n)∗(n−1)n
⟹365n−365>366n−n2⟹365n−365>366n−n2,
⟹n2−n−365>0⟹n2−n−365>0
⟹(n−(1+(√1461)2)∗(n−(1−(√1461)2)>0⟹(n−(1+(1461)2)∗(n−(1−(1461)2)>0
⟹n=(1+(√1461)2=19.6115148536⟹n=(1+(1461)2=19.6115148536 (∵n>0∵n>0)
⟹n=20⟹n=20 (ceiling of computed value)
Hence the 20th20th position maximizes the chances.
"
https://docs.google.com/spreadsheets/d/1dMXhw7qxKa96hXN94jjZj5mzWdTgzXxMG91vpJpPPag/edit#gid=0
The percent chance of stopping at each point is the difference of percentages of the total probability of having a birthday at that point and the point before. This doc shows that the maximum percentage for this difference is at 20 people, so this is the greatest chance of stopping.
The percent chance of stopping at each point is the difference of percentages of the total probability of having a birthday at that point and the point before. This doc shows that the maximum percentage for this difference is at 20 people, so this is the greatest chance of stopping.
Good!https://docs.google.com/spreadsheets/d/1dMXhw7qxKa96hXN94jjZj5mzWdTgzXxMG91vpJpPPag/edit#gid=0
The percent chance of stopping at each point is the difference of percentages of the total probability of having a birthday at that point and the point before. This doc shows that the maximum percentage for this difference is at 20 people, so this is the greatest chance of stopping.
3 points for marketing, 2 for engineering, 1 for finance
Yes. 3 marketing, 2 finance 2 engineering. M&Ms are still open.fuck you phone
6. The Notebook
bring a good teambuilder for the next wave, releasing at noon!
There were 88 M&Ms in the glass. Marketing submitted 75, off by 13. Engineering guessed 102, off by 14. Finance guessed 96, off by 8, winning a point! Marketing and Finance are tied at 3 points a piece, engineering have 2. The final three points will be assigned in three hours. See you soon!
Task 9:
Complete the following PS challenges. Save your replays and submit in thread once you are finished. First to submit wins!
On a OU ladder match on PS, crit 5 times in consecutive turns, then win the match. You may not use the moves Storm Throw, Frost Breath, Zippy Zap, Surging Strikes, or Wicket Blow. The opponent may not forfeit.
On a ladder gen 8 randbats match on PS, lose five of your pokemon before the opponent loses one. Then, win the match. The opponent may not forfeit.
On a OU ladder match on PS, win using only the move metronome. The opponent may not forfeit.
Task 10:
You are given several water tanks that each have two faucets (which are identical). You are told that each water tank has the following property: should one faucet be on, the tank will take exactly 1 hour and 4 minutes to deplete. Should two faucets be on, then the tank depletes exactly twice as quickly. However, the tank does not deplete at a uniform rate. For example, if one faucet is on, then half the water might be gone in the first 4 minutes, but the other half might take an hour to deplete. The rate at which different water tanks deplete also can vary, though they all will deplete in 1 hour and 4 minutes if one faucet is on (32 min if two are on from the start).
How can you measure a time of 1 minute, using only these tanks? How many water tanks are required?
Guess as many times as you'd like for this question, with one guess per post.
Task 11:
What movie is the below image from?
Each tribe may guess once every 15 minutes.

Complete the following PS challenges. Save your replays and submit in thread once you are finished. First to submit wins!
On a OU ladder match on PS, crit 5 times in consecutive turns, then win the match. You may not use the moves Storm Throw, Frost Breath, Zippy Zap, Surging Strikes, or Wicket Blow. The opponent may not forfeit.
On a ladder gen 8 randbats match on PS, lose five of your pokemon before the opponent loses one. Then, win the match. The opponent may not forfeit.
On a OU ladder match on PS, win using only the move metronome. The opponent may not forfeit.
Task 10:
You are given several water tanks that each have two faucets (which are identical). You are told that each water tank has the following property: should one faucet be on, the tank will take exactly 1 hour and 4 minutes to deplete. Should two faucets be on, then the tank depletes exactly twice as quickly. However, the tank does not deplete at a uniform rate. For example, if one faucet is on, then half the water might be gone in the first 4 minutes, but the other half might take an hour to deplete. The rate at which different water tanks deplete also can vary, though they all will deplete in 1 hour and 4 minutes if one faucet is on (32 min if two are on from the start).
How can you measure a time of 1 minute, using only these tanks? How many water tanks are required?
Guess as many times as you'd like for this question, with one guess per post.
Task 11:
What movie is the below image from?
Each tribe may guess once every 15 minutes.
Birdbox 11
Point. Marketing with 4 points secure immunity!Birdbox 11
task 10: let the tanks be A, B, C, D, E, F, and G
turn on both faucets in A, while turning on one faucet in the rest of the tanks.
When A is filled, (C has 32 minutes left in tank if left at one faucet), turn on the second faucet in B.
When B is filled, (D has 16 minutes left in tank if left at one faucet), turn on the second faucet in C.
When C is filled, (E has 8 minutes left in tank if left at one faucet), turn on second faucet in D.
When D is filled, (F has 4 minutes left in tank if left at one faucet), turn on second faucet in E
When E is filled, (G has 2 minutes left in tank if left at one faucet) turn on second faucet in F.
When F is filled, (G has one minute left in tank if left at one faucet), start your timer and end it once G is filled to time one minute.
turn on both faucets in A, while turning on one faucet in the rest of the tanks.
When A is filled, (C has 32 minutes left in tank if left at one faucet), turn on the second faucet in B.
When B is filled, (D has 16 minutes left in tank if left at one faucet), turn on the second faucet in C.
When C is filled, (E has 8 minutes left in tank if left at one faucet), turn on second faucet in D.
When D is filled, (F has 4 minutes left in tank if left at one faucet), turn on second faucet in E
When E is filled, (G has 2 minutes left in tank if left at one faucet) turn on second faucet in F.
When F is filled, (G has one minute left in tank if left at one faucet), start your timer and end it once G is filled to time one minute.
task 10: let the tanks be A, B, C, D, E, F. (6 are required)
turn on both faucets in A, while turning on one faucet in the rest of the tanks.
When A is filled, (C has 32 minutes left in tank if left at one faucet), turn on the second faucet in B.
When B is filled, (D has 16 minutes left in tank if left at one faucet), turn on the second faucet in C.
When C is filled, (E has 8 minutes left in tank if left at one faucet), turn on second faucet in D.
When D is filled, (F has 4 minutes left in tank if left at one faucet), turn on second faucet in E
When E is filled, (F has 2 minutes left in tank if left at one faucet) turn on second faucet in F and start your timer, and end it once F is full.
turn on both faucets in A, while turning on one faucet in the rest of the tanks.
When A is filled, (C has 32 minutes left in tank if left at one faucet), turn on the second faucet in B.
When B is filled, (D has 16 minutes left in tank if left at one faucet), turn on the second faucet in C.
When C is filled, (E has 8 minutes left in tank if left at one faucet), turn on second faucet in D.
When D is filled, (F has 4 minutes left in tank if left at one faucet), turn on second faucet in E
When E is filled, (F has 2 minutes left in tank if left at one faucet) turn on second faucet in F and start your timer, and end it once F is full.
correct. Finance wins!task 10: let the tanks be A, B, C, D, E, F. (6 are required)
turn on both faucets in A, while turning on one faucet in the rest of the tanks.
When A is filled, (C has 32 minutes left in tank if left at one faucet), turn on the second faucet in B.
When B is filled, (D has 16 minutes left in tank if left at one faucet), turn on the second faucet in C.
When C is filled, (E has 8 minutes left in tank if left at one faucet), turn on second faucet in D.
When D is filled, (F has 4 minutes left in tank if left at one faucet), turn on second faucet in E
When E is filled, (F has 2 minutes left in tank if left at one faucet) turn on second faucet in F and start your timer, and end it once F is full.
With a score of 4 Finance, 4 marketing, 2 engineering, the challenge ends. Engineering is sent to performance review.








